پردازش تصویر با پایتون-کانولوشن
 Convolution
Convolution
کانولوشن در حوزه مکان سری حاصلضرب دو ماتریس، که عناصر یکی(کرنل ) ، برعکس شده و بر روی دیگری پیمایش میکند یا گام بر میدارد. پیمایش یا گام برداشتن بر روی تک تک عناصر تصویر ورودی است . برای هر گام عناصر مربوطه در هر دو ماتریس را ضرب میکنیم سپس آنها را جمع کرده تا یک عنصر جدید بدست آوریم. این کار آنقدر میشود تا این ماتریس کوچک به عنوان ماسک ، تمام عناصر موجود در ماتریس ورودی یا تصویر را مرور کند. عناصرموجود درماتریس جدید حاصل کانولوشن است.
۱٫کانولوشن حوزه مکان
یکی از عملگر های مهم در پردازش تصویر و سیگنال، کانولوشن است که برروی دو سیگنال یک بعدی یا دو بعدی عمل میکند: یعنی می توانید یک سیگنال (یا تصویر) را به عنوان ورودی و دیگری ( هسته) را به عنوان فیلتر روی تصویر ورودی، در نظر بگیرید که سرانجام باعث تولید تصویر خروجی میشود.
(بنابراین کانولوشن دو عکس را به عنوان ورودی می گیرد و تصویر سومی را به عنوان خروجی تولید می کند. )
کانولوشن در حوزه مکان عملگر ضرب هم معنی میشود. در واقع یک مفهوم فوق العاده مهم در بسیاری از زمینه های ریاضی و مهندسی (از جمله بینایی کامپیوتر است).
کانولوشن بر روی سیگنال یک بعدی را مشاهده میکنید :

می توانیم کانولوشن را در سیگنالهای ۲D نیز اعمال کنیم. برای کانولوشن ۲D، هسته روی هر پیکسل از تصویر حرکت میکندیعنی پیمایش میکند و عمل ضرب تصویر ورودی و هسته، و اضافه کردن آنها – نتیجه ارزش جدیدی از تصویر است.
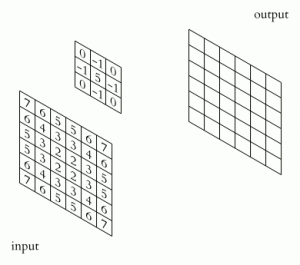
این قسمت یک مثال ساده از کانولوشن در فضایی ۲D است. تعریف کانولوشن ۲D و چگونگی پیمایش در ۲D در اینجا توضیح داده شده است.
![ورودی x[m,n]](http://www.songho.ca/dsp/convolution/files/conv_img12a.gif)
ورودی
![کرنل h[m,n]](http://www.songho.ca/dsp/convolution/files/conv_img15.gif)
هسته
![خروجی y[m,n]](http://www.songho.ca/dsp/convolution/files/conv_img13a.gif)
خروجی
![y[0,0]](http://www.songho.ca/dsp/convolution/files/conv_img16.gif)
![y[0,0]](http://www.songho.ca/dsp/convolution/files/conv2d_eq07.gif)
![y[1,0]](http://www.songho.ca/dsp/convolution/files/conv_img17.gif)
![y[1,0]](http://www.songho.ca/dsp/convolution/files/conv2d_eq08.gif)
![y[2,0]](http://www.songho.ca/dsp/convolution/files/conv_img18.gif)
![y[2,0]](http://www.songho.ca/dsp/convolution/files/conv2d_eq09.gif)
![y[1,1]](http://www.songho.ca/dsp/convolution/files/conv_img20.gif)
![y[1,1]](http://www.songho.ca/dsp/convolution/files/conv2d_eq11.gif)
![y[2,1]](http://www.songho.ca/dsp/convolution/files/conv_img21.gif)
![y[1,1]](http://www.songho.ca/dsp/convolution/files/conv2d_eq11.gif)
![y[2,1]](http://www.songho.ca/dsp/convolution/files/conv_img21.gif)
![y[2,1]](http://www.songho.ca/dsp/convolution/files/conv2d_eq12.gif)
![y[0,2]](http://www.songho.ca/dsp/convolution/files/conv_img22.gif)
![y[0,2]](http://www.songho.ca/dsp/convolution/files/conv2d_eq13.gif)
![y[1,2]](http://www.songho.ca/dsp/convolution/files/conv_img23.gif)
![y[1,2]](http://www.songho.ca/dsp/convolution/files/conv2d_eq14.gif)
![y[2,2]](http://www.songho.ca/dsp/convolution/files/conv_img24.gif)
![y[2,2]](http://www.songho.ca/dsp/convolution/files/conv2d_eq15.gif)
